Vektor adalah besaran yang memiliki arah. Besaran ini memiliki bentuk operasi matematis khusus.
Daftar isi
Pengertian Vektor
Besaran berdasarkan arahnya terdiri dari:
- Besaran skalar, besaran yang tak punya arah. Contoh: massa (m), panjang (L), waktu (t), kelajuan (v), massa jenis (ρ).
- Besaran vektor, besaran yang punya arah. Contoh: gaya (F), Percepatan (a), kecepatan (v). Penulisan besaran vektor ditulis dengan benar dengan simbol panah di atas hurusnya.
\vec{F}\vec{a}\vec{v}\vec{B}Vektor diberi nama dengan huruf kecil bergaris atas atau menyebut titik pangkal dan ujungnya.
- Anak panah menunjuk arah yang ditunjuk vektor.
- Besar kecilnya vektor dilambangkan dengan besar kecilnya anak panah.
Nilai arah vektor:
- Vektor positif pada koordinat kartesius arahnya ke atas (terhadap y) atau ke kanan (terhadap x).
- Vektor negatif pada koordinat kartesius arahnya ke bawah (terhadap y) atau ke kiri (terhadap x).
- Vektor memiliki resultan yang merupakan hasil dari penjumlahan, pengurangan atau perkaliannya.
A. Penjumlahan Vektor
Penjumlahan dan pengurangan vektor digunakan untuk mencari resultan vektor. Resultan vektor dapat dicari dengan menghubungkan pangkal vektor awal dengan ujung vektor akhir.
1. Metode Segitiga
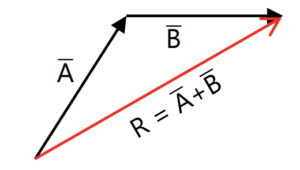
2. Metode Jajaran Genjang
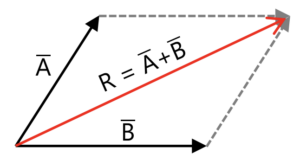
3. Metode Poligon
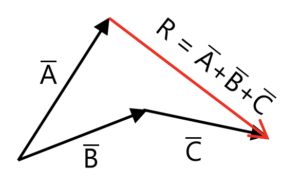
Pengurangan vektor dapat menggunakan sifat operasi hitung:
R = A̅ – B̅ = A̅ + (-B̅) (berbalik arah)
B. Metode Analitik
Sebuah vektor dapat diuraikan menjadi dua buah vektor pada sumbu horizontal (x) dan sumbu vertikal (y). Vektor tersebut terurai menjadi komponen x dan y yang saling tegak lurus dan memiliki resultan dengan arah yang merupakan vektor yang terurai itu sendiri.
Cara menentukan komponen vektor:
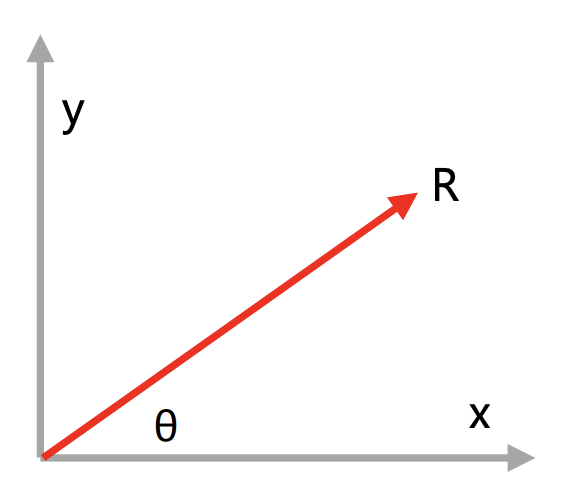
x = R cos θ
y = R sin θ
R = \sqrt{x^2+y^2}\tan \theta=\frac{x}{y}Misalkan dua buah vektor membentuk sudut sebesar θ seperti pada gambar di bawah
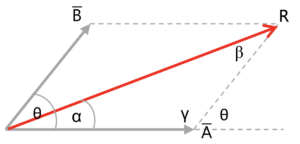
Resultan vektor dihitung menggunakan persamaan kosinus:
R =\sqrt{A^2+B^2+2AB \cos \alpha }Arah resultan terhadap sumbu x dapat dihitung dengan persamaan sinus:
\frac{B}{\sin \alpha} = \frac{A}{\sin \beta} = \frac{R}{\sin \gamma}C. Perkalian Vektor
Perkalian vektor terdiri dari dua, yaitu perkalian titik (dot), dan perkalian silang (cross). Bentuk penulisan vektor:
- Vektor posisi, ditulis dalam notasi vektor terhadap titik acuan. Contoh: vektor posisi titik A dari O adalah OA.
- Vektor basis, ditulis dalam vektor satuan. Vektor satuan sumbu x adalah i, sumbu y adalah j, dan sumbu z adalah k.
a̅ = x i + y j + z k
Panjang/nilai skalar dari vektor yang ditulis dalam vektor basis adalah:
|\bar{a}|=\sqrt{x^2+y^2+z^2}1. Dot Produk
Perkalian skalar/titik (•) menghasilkan besaran skalar, memiliki definisi:
a̅ • b̅ = |a||b| cos θ
perkalian skalar dengan vektor basis dengan a̅ = (x1, y1, z1) dan b̅ = (x2, y2, z2) diketahui dapat dihitung
a̅ • b̅ = x1x2+y1y2+z1z2
sifat perkalian skalar
- a • a = |a|2
- i • i = j • j = k • k = 1
- i • j = j • k = k • i = 0
- a • b = b • a
- a • (b ± c) = (a • b) ± (a • c)
- (m.a) • (n.b) = (m.n)(a • b)
- a • b = 0, maka a ┴ b
2. Cross Produk
Perkalian vektor/silang (×) menghasilkan besaran vektor yang tegak lurus terhadap dua vektor yang dikali silang, memiliki definisi:
a̅ × b̅ = |a||b|sinθ e̅
Perkalian vektor dengan vektor basis dengan a̅ = (x1, y1, z1) dan b̅ = (x2, y2, z2) diketahui dapat dihitung:
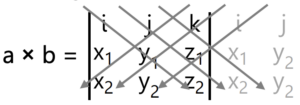
a̅ × b̅ = (y1.z2 – y2.z1) i + (z1.x2 – z2.x1) j + (y1.x2 – y2.x1) k
sifat perkalian vektor
- a × a = 0
- vektor satuan
- i × i = j × j = k × k = 0
- i × j = k
- j × k = i
- k × i = j
- j × i = -k
- k × j = -i
- i × k = -j
- a × b ≠ b × a
- a × b = -(b × a)
- a × (b ± c) = (a × b) ± (a × c)
- (b ± c) × a = (b × a) ± (c × a)
Sudut dua vektor dapat dicari menggunakan perkalian skalar.
\cos \theta =\frac{\bar{a}.\bar{b}}{|\bar{a}|.|\bar{b}|}
Leave a Reply
You must be logged in to post a comment.