Structure of Observed Learning Outcomes atau biasa dikenal dengan nama Taksonomi SOLO adalah kerangka tingkat pemahaman atau kualitas hasil belakar peserta didik. Taksonomi ini digunakan dalam menilai kualitas pembelajaran peserta didik tidak sebatas Benar atau Salah.
Daftar isi
Taksonomi SOLO
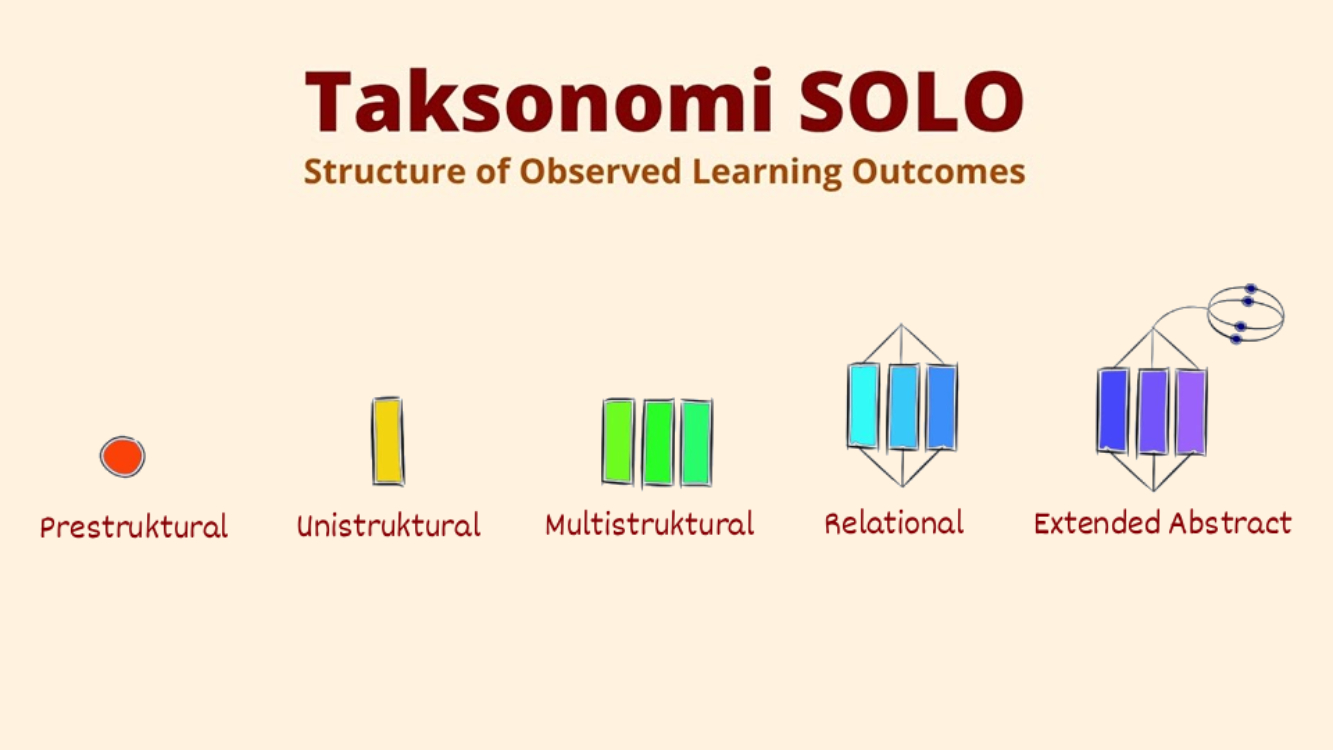
Taksonomi SOLO merupakan model evaluasi yang dikembangkan oleh John BIggs dan Kevin Collis pada tahun 1982. Model evaluasi dilaksanakan melalui pengukuran kompleksitas pengetahuan peserta didik terhadap materi pembelajaran. Kompleksitas dibedakan ke dalam lima tingkatan yakni:
- Prestructural
- Unistruktural
- Multistriktural
- Relational
- Extended Abstract
A. Prestruktural (Prestructural)
Prastruktural adalah tahap dimana peserta didik dianggap tidak memiliki pemahaman dan pengetahuan yang relevan terkait dengan topik yang sedang dipelajari. Peserta didik memberikan respon yang tidak relevan terhadap tugas-tugas yang diberikan.
- Peserta didik tidak memahami pertanyaan atau tugas yang diberikan
- Respon yang ditunjukkan tidak relevan
- Tidak ada hubungan yang logis antara jawaban dan pertanyaan.
2. Unistruktural (Unistructural)
Siswa hanya memahami satu aspek atau elemen sederhana dari konsep yang dipelajari. Pemahaman mereka terbatas pada fakta atau prosedur tunggal tanpa menghubungkannya dengan konsep lain.
– Ciri-ciri:
– Fokus pada satu fakta, langkah, atau ide.
– Tidak ada koneksi dengan konsep lain atau pemahaman yang lebih luas.
3. Tingkat Multistruktural (Multistructural)
Siswa mulai memahami beberapa aspek atau elemen dari konsep, tetapi pemahaman ini masih terpisah-pisah dan tidak terintegrasi. Mereka dapat menyebutkan beberapa fakta atau langkah, tetapi tidak menghubungkannya secara koheren.
– Ciri-ciri:
– Mampu menyebutkan beberapa fakta atau langkah prosedur.
– Tidak ada hubungan yang jelas antar elemen yang disebutkan.
– Pemahaman masih bersifat permukaan.
4. Tingkat Relasional (Relational)
Pada tingkat ini, siswa mampu menghubungkan berbagai elemen atau aspek dari konsep yang dipelajari menjadi suatu pemahaman yang terintegrasi. Mereka dapat menjelaskan hubungan antar elemen dan bagaimana elemen-elemen tersebut membentuk keseluruhan konsep.
– Ciri-ciri:
– Menunjukkan hubungan antar fakta atau langkah-langkah.
– Pemahaman lebih mendalam dan terstruktur.
– Mampu menjelaskan “mengapa” di balik suatu proses.
5. Tingkat Abstrak Diperluas (Extended Abstract)
Ini adalah tingkat tertinggi dalam taksonomi SOLO, di mana siswa tidak hanya memahami dan mengintegrasikan konsep, tetapi juga mampu menggeneralisasi, mengabstraksi, atau menerapkannya dalam konteks baru yang lebih luas atau kompleks. Pemahaman mereka bersifat kreatif dan inovatif.
– Ciri-ciri:
– Mampu mengaitkan konsep dengan situasi baru atau berbeda.
– Menunjukkan pemikiran kritis, kreatif, atau hipotetis.
– Dapat membuat generalisasi atau teori berdasarkan pemahaman.
Contoh Kasus
Tugas : Jelaskan bagaiman cara menyelesaikan persamaan linier
2x + 3 = 7
Respon Fase Extended Abstract :
Solusi dari dari 2x + 3 = 7 yang pertama adalah membuat variabel x sendiri pada kedua rua sehingga cara yang paling tepat adalah mengurangkan 3 di kedua sisi sehingga persamaan menjadi
2x + 3 – 3 = 7 – 3
2x = 4
Prinsip ini merupakan prinsip universal untuk semua persamaan dimana setiap yang dilakukan di ruas kiri juga harus dilakukan diruas kana karena ada tanda “sama dengan (=)”. Prinsip ini juga dilanjutkan untuk menunjukkan nilai x yang sebenarnya yakni dengan membagi kedua ruas dengan 2.
2x / 2= 4/2
dengan demikin nilai x = 2.
*(Siswa tidak hanya menjelaskan langkah-langkah, tetapi juga menggeneralisasi prinsip ke semua persamaan linear dan menghubungkannya dengan konteks lain seperti pemrograman atau aplikasi praktis.)*
—
### Ringkasan Karakteristik dan Perbandingan
| **Tingkat** | **Fokus Pemahaman** | **Contoh dalam Persamaan Linear** |
|————————–|———————————————|————————————————————————————————-|
| Prestruktural | Tidak paham, respons tidak relevan | “Persamaan itu seperti grafik.” |
| Unistruktural | Satu aspek/fakta sederhana | “Kurangi 3 dari 7.” |
| Multistruktural | Beberapa aspek, tapi tidak terhubung | “Kurangi 3 dari 7, lalu bagi dengan 2. Jadi x = 2.” |
| Relasional | Hubungan antar aspek, pemahaman terintegrasi | “Kurangi 3 untuk isolasi x, lalu bagi dengan 2 untuk mendapatkan x = 2, menjaga keseimbangan.” |
| Abstrak Diperluas | Generalisasi, aplikasi ke konteks baru | “Prinsip isolasi variabel berlaku untuk semua persamaan linear dan bisa diterapkan di bidang lain.” |
—
### Manfaat Taksonomi SOLO dalam Pendidikan
1. **Penilaian Pemahaman Siswa**: Guru dapat mengevaluasi sejauh mana siswa memahami suatu konsep, dari sekadar menghafal hingga menerapkannya secara kreatif.
2. **Desain Pembelajaran**: Membantu guru merancang tugas atau pertanyaan yang mendorong siswa mencapai tingkat pemahaman yang lebih tinggi (misalnya, dari multistruktural ke relasional).
3. **Pendekatan Diferensiasi**: Memungkinkan guru mengidentifikasi kebutuhan individu siswa dan memberikan intervensi yang sesuai dengan tingkat pemahaman mereka.
4. **Fokus pada Kualitas**: Berbeda dengan taksonomi Bloom yang berfokus pada jenis kognitif, SOLO menekankan struktur dan kedalaman pemahaman, sehingga lebih fleksibel untuk berbagai mata pelajaran.
—
### Contoh Penerapan dalam Desain Soal
Untuk mendorong siswa mencapai tingkat yang lebih tinggi dalam taksonomi SOLO, guru dapat merancang soal dengan tingkat kesulitan yang sesuai. Misalnya:
– **Unistruktural**: “Apa langkah pertama untuk menyelesaikan 2x + 3 = 7?”
– **Multistruktural**: “Tuliskan langkah-langkah untuk menyelesaikan 2x + 3 = 7.”
– **Relasional**: “Jelaskan mengapa kita harus mengurangi 3 dari kedua sisi dalam persamaan 2x + 3 = 7.”
– **Abstrak Diperluas**: “Bagaimana konsep menyelesaikan persamaan linear dapat digunakan untuk memecahkan masalah di bidang ekonomi atau teknologi?”
—
### Kesimpulan
Taksonomi SOLO adalah alat yang sangat berguna untuk memahami tingkat pemahaman siswa secara struktural, dari ketidakpahaman hingga kemampuan menggeneralisasi konsep ke konteks baru. Dengan memahami tingkatan ini, pendidik dapat merancang strategi pembelajaran yang lebih efektif dan menilai kemajuan siswa secara lebih akurat. Contoh konkret dalam persamaan linear di atas menunjukkan bagaimana SOLO dapat diterapkan dalam mata pelajaran spesifik untuk mengukur dan mendorong pemahaman yang lebih mendalam.
Leave a Reply
You must be logged in to post a comment.