Daftar isi
Gerak Melingkar Beraturan
Bab I. Pendahuluan
A. Latar Belakang
Gerak adalah suatu perubahan tempat kedudukan pada suatu benda dari titik keseimbangan awal. Sebuah benda dikatakan bergerak jika benda itu berpindah kedudukan terhadap benda lainnya baik perubahan kedudukan yang menjauhi maupun yang mendekati.
Fisika adalah ilmu yang mempelajari benda-benda serta fenomena dan keadaan yang terkait dengan benda-benda tersebut. Untuk menggambarkan suatu fenomena yang terjadi atau dialami suatu benda, maka didefinisikan berbagai besaran-besaran fisika. Besaran-besaran fisika ini misalnya panjang, jarak, massa, waktu, gaya, kecepatan, temperatur, intensitas cahaya, dan sebagainya. Terkadang nama dari besaran-besaran fisika tadi memiliki kesamaan dengan istilah yang dipakai dalam keseharian, tetapi perlu diperhatikan bahwa besaran-besaran fisika tersebut tidak selalu memiliki pengertian yang sama dengan istilah-istilah keseharian. Seperti misalnya istilah gaya, usaha, dan momentum, yang memiliki makna yang berbeda dalam keseharian atau dalam bahasa-bahasa sastra. Misalnya, “Anak itu bergaya.
Pada makalah ini akan dibahas tentang gerak melingkar beraturan dalam Fisika beserta Besaran-besarannya.
B. Tujuan
- Untuk mengetahui tentang pengertian gerak melingkar beraturan dan besaran-Besaran dalam gerak Melingkar Beraturan
- Untuk mengetahui tentang kecepatan sudut/kecepatan angular gerak melingkar beraturan dan contoh soal.
Bab II. Pembahasan
A. Pengertian Gerak Melingkar Beraturan
Gerak Melingkar Beraturan (GMB) adalah gerak yang lintasannya berbentuk lingkaran dengan laju konstan dan arah kecepatan tegak lurus terhadap arah percepatan. Arah kecepatan terus berubah sementara benda bergerak dalam lingkaran tersebut, tampak seperti pada gambar disamping. Oleh karena percepatan didefinisikan sebagai besar perubahan kecepatan, perubahan arah kecepatan menyebabkan percepatan sebagaimana juga perubahan besar kecepatan. Dengan demikian, benda yang mengelilingi sebuah lingkaran terus dipercepat, bahkan ketika lajunya tetap konstan (v1= v2= v).
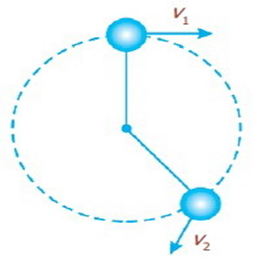
Beberapa lambang yang biasa ditemukan dalam GMB antara lain :
Keterangan
f : frekuensi (Hz)
T : Periode (s)
n : banyak putaran
t : waktu (s)
ω : frekuensi sudut (rad/s)
v : kecepatan (m/s
r : jari-jari lintasan (m)
Frekuensi (f) dan periode (T) dalam GMB :
\theta =\frac{s}{R}sesuai dengan keterangan lambang2 di atas berarti :
Frekuensi = banyaknya putaran/waktu
Periode = waktu/banyaknya putaran
Rumus Kecepatan Sudut (ω)
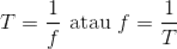
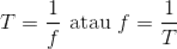
Keterangan :
ω = Kecepatan sudut (rad/s)
f = frekuensi (Hz)
T = periode (s)
π = 3,14 atau 22/7 atau tetap/tidak diganti angka
B. Besaran-Besaran Dalam Gerak Melingkar Beraturan
1. Periode Dan Frekuensi Gerak Melingkar Beraturan
Sebuah partikel/benda yang bergerak melingkar baik gerak melingkar beraturan ataupun yang tidak beraturan, geraknya akan selalu berulang pada suatu saat tertentu. Dengan memerhatikan sebuah titik pada lintasan geraknya, sebuah partikel yang telah melakukan satu putaran penuh akan kembali atau melewati posisi semula. Gerak melingkar sering dideskripsikan dalam frekuensi ( f ), yaitu jumlah putaran tiap satuan waktu atau jumlah putaran per sekon. Sementara itu, periode (T ) adalah waktu yang diperlukan untuk menempuh satu putaran.
Hubungan antara periode (T ) dan frekuensi ( f ) adalah:
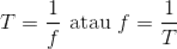
dengan:
T = periode (s)
f = frekuensi (Hz)
Sebagai contoh, jika sebuah benda berputar dengan frekuensi 3 putaran/sekon, maka untuk melakukan satu putaran penuh, benda itu memerlukan waktu 1/3 sekon. Untuk benda yang berputar membentuk lingkaran dengan laju konstan ν, dapat kita tuliskan:
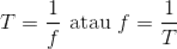
Hal ini disebabkan dalam satu putaran, benda tersebut menempuh satu keliling lingkaran (= 2 π R).
2. Posisi Sudut (θ) Gerak Melingkar Beraturan
Gambar dibawah melukiskan sebuah titik P yang berputar terhadap sumbu yang tegak lurus terhadap bidang gambar melalui titik O. Titik P bergerak dari A ke B dalam selang waktu t. Posisi titik P dapat dilihat dari besarnya sudut yang ditempuh, yaitu θ yang dibentuk oleh garis AB terhadap sumbu x yang melalui titik O. Posisi sudut θ diberi satuan radian (rad). Besar sudut satu putaran adalah 360° = 2 θ radian.
Jika θ adalah sudut pusat lingkaran yang panjang busurnya s dan jari-jarinya R, diperoleh hubungan:
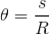
dengan:
θ = lintasan/posisi sudut (rad)
s = busur lintasan (m)
R = jari-jari (m)
C. Kecepatan Sudut/Kecepatan Angular Gerak Melingkar Beraturan
Dalam gerak melingkar beraturan, kecepatan sudut atau kecepatan anguler untuk selang waktu yang sama selalu konstan. Kecepatan sudut didefinisikan sebagai besar sudut yang ditempuh tiap satu satuan waktu. Untuk partikel yang melakukan gerak satu kali putaran, didapatkan sudut yang ditempuh θ =2 π dan waktu tempuh t = T. Berarti, kecepatan sudut ( ω) pada gerak melingkar beraturan dapat dirumuskan:
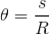
dengan:
ω = kecepatan sudut (rad/s)
T = periode (s)
f = frekuensi (Hz)
D. Contoh Soal :
1. Sebuah partikel bergerak melingkar dengan kelajuan sudut konstan 10 rad/s. Tentukan (a) kelajuan sudut partikel setelah 10 sekon (b) sudut yang dikelilingi partikel setelah 10 sekon.
Pembahasan
Jawab :
(a) kelajuan sudut setelah 10 sekon
Partikel bergerak melingkar beraturan = partikel bergerak dengan kecepatan sudut tetap. Jadi kelajuan sudut setelah 10 sekon tetap 10 radian/sekon.
(b) sudut yang dikelilingi setelah 10 sekon
Kelajuan sudut konstan 10 radian / sekon artinya setiap 1 sekon, partikel mengelilingi sudut 10 radian. Setelah 2, partikel telah mengelilingi sudut 2 x 10 = 20 radian. Setelah 10 sekon, partikel telah mengelilingi sudut 10 x 10 radian = 100 radian.
2. Sebuah titik pada tepi silinder bergerak melingkar dengan kelajuan konstan 10 m/s. Jari-jari silinder = 1 meter. Tentukan (a) kelajuan tepi silinder 5 sekon kemudian (b) jarak yang ditempuh tepi silinder 5 sekon kemudian (c) percepatan sentripetal titik yang berjarak 0,5 meter dan 1 meter dari poros alias sumbu putar.
Pembahasan
Diketahui :
Jari-jari silinder (r) = 1 meter
Kelajuan tepi silinder (v) = 10 m/s
Ditanya :
(a) kelajuan tepi silinder (v) setelah t = 5 sekon
(b) jarak tempuh (s) tepi silinder setelah t = 5 ekon
(c) percepatan sentripetal (as)
Jawab :
(a) kelajuan titik pada tepi silinder setelah 5 sekon
Silinder bergerak melingkar dengan kelajuan konstan karenanya 5 sekon kemudian, kelajuan tepi silinder tetap 10 meter/sekon
(b) jarak tempuh titik pada tepi silinder setelah 5 sekon
Tanpa rumus
Kelajuan 10 meter/sekon artinya setiap 1 sekon, titik pada tepi selinder bergerak sejauh 10 meter. Setelah 1 sekon, titik pada tepi silinder bergerak sejauh 10 meter. Setelah 2 sekon, titik pada tepi silinder bergerak sejauh 20 meter. Setelah 5 sekon, titik pada tepi silinder bergerak melingkar sejauh 50 meter.
Menggunakan rumus :
v = s / t
s = v t = (10)(5) = 50 meter
(c) percepatan sentripetal (as)
Percepatan sentripetal sebuah titik berjarak 0,5 meter dari poros adalah :
as = v2 / r = 102 / 0,5 = 100 / 0,5 = 200 m/s2
Percepatan sentripetal sebuah titik berjarak 1 meter dari poros adalah :
as = v2 / r = 102 / 0,5 = 100 / 1 = 100 m/s2
3. Sebuah meja putar berjari-jari 2 meter bergerak kelajuan sudut konstan 60 rpm. Tentukan (a) besar kecepatan sudut meja putar 2 sekon kemudian (b) sudut yang dikelilingi meja putar setelah 1 menit (b) kelajuan tangensial, percepatan sentripetal dan jarak yang ditempuh suatu titik berjarak 1 meter dari poros alias sumbu putar (c) kelajuan tangensial, percepatan sentripetal dan jarak yang ditempuh suatu titik pada tepi meja putar.
Pembahasan
Diketahui :

Jawab :
(a) kelajuan sudut ( ) setelah 2 sekon
Kelajuan sudut konstan karenanya setelah 2 sekon kelajuan sudut meja putar tetap 6,28 radian / sekon
(b) Sudut ( ) yang dikelilingi meja putar setelah 1 menit
Kelajuan sudut 1 putaran / sekon artinya setiap 1 sekon meja putar melakukan 1 putaran. Setelah 60 sekon, meja putar melakukan 60 putaran. Atau dengan cara lain,
Kelajuan sudut 6,28 radian / sekon artinya setiap 1 sekon meja putar mengelilingi sudut 6,28 radian. Setelah 60 sekon, meja putar mengelilingi sudut 376,8 radian.
4. Roda sebuah mobil selalu melakukan 120 putaran setiap 60 sekon. Berapa kelajuan sudut roda ? Nyatakan dalam : (a) revolution per minute (rpm) atau putaran per menit (b) derajat per sekon (o/s) (c) radian per sekon (rad/s)
Pembahasan
(a) kelajuan sudut roda dalam satuan putaran / menit (rpm)
120 putaran / 60 sekon = 120 putaran / 1 menit = 120 putaran / menit =
120 rpm
(b) kelajuan sudut roda dalam satuan derajat / sekon (o/s)
1 putaran = 360o, 120 putaran = 43200o
Jadi 120 putaran / 60 sekon = (120)(360o) / 60 sekon = 43200o / 60 sekon
= 720o/sekon
(c) kelajuan sudut roda dalam satuan radian/sekon (rad/s)
1 putaran = 6,28 radian
Jadi 120 putaran / 60 sekon = (120)(6,28) radian / 60 sekon = 753,6 radian / 60 sekon = 12,56 radian/sekon
BAB III
PENUTUP
A. Kesimpulan
Gerak Melingkar Beraturan (GMB) adalah gerak yang lintasannya berbentuk lingkaran dengan laju konstan dan arah kecepatan tegak lurus terhadap arah percepatan. Arah kecepatan terus berubah sementara benda bergerak dalam lingkaran tersebut. Oleh karena percepatan didefinisikan sebagai besar perubahan kecepatan, perubahan arah kecepatan menyebabkan percepatan sebagaimana juga perubahan besar kecepatan. Dengan demikian, benda yang mengelilingi sebuah lingkaran terus dipercepat, bahkan ketika lajunya tetap konstan (v1= v2= v).
Fisika adalah ilmu yang mempelajari benda-benda serta fenomena dan keadaan yang terkait dengan benda-benda tersebut. Untuk menggambarkan suatu fenomena yang terjadi atau dialami suatu benda, maka didefinisikan berbagai besaran-besaran fisika. Besaran-besaran fisika ini misalnya panjang, jarak, massa, waktu, gaya, kecepatan, temperatur, intensitas cahaya, dan sebagainya.
B. Saran
Demikianlah makalah mengenai gerak melingkar beraturan yang dapat penulis sampaikan, penulis berharap kepada pembaca agar dapat memberikan penulis kritikan maupun masukkan yang positif demi penyempurnaan makalah ini. Semoga makalah ini memberikan faedah bagi kita semua.
DAFTAR PUSTAKA
http://gurumuda.net/contoh-soal-gerak-melingkar-beraturan.htm
http://nurayuannisa.blogspot.com/2013/08/contoh-soal-dan-penyelesaian-gerak.html
Gerak Melingkar
http://e-learningman1mdn.blogspot.com/2011/11/gerak-melingkar.html
Leave a Reply
You must be logged in to post a comment.