Lingkaran

LINGKARAN

Lingkaran merupakan bentuk kurva sederhana tertutup yang lain selain segi banyak. Lingkaran adalah himpunan titik-titik pada suatu bidang yang berjarak sama, dari suatu titik-titik pada suatu bidang yang berjarak sama, dari suatu titik tertentu. Titik tertentu tersebut dinamakan titik pusat lingkaran.

Sifat-sifatLingkaran

Ø Panjang diameter lingkaran dua kali panjan gjari-jarinya

Ø Panjangjari-jarinyasetengahpanjangdiameternya.

Ø Besarsudutnya 360°

Ø Sumbusimetritakterhingga

Ø Memilikisatutitikpusatlingkaran

Ø Tidakmempunyaisimetrilipatdansimetriputar.

1. Jari-jari dan Diameter Lingkaran

Perhatikanlah gambar lingkaran dengan titik pusat Oberikut.

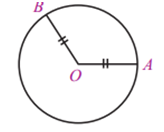
Jarak dari titik pusat ke setiap titik pada lingkaran dinamakan jari-jari lingkaran. Pada gambar tersebut jarak titik Oke titik Asama dengan jarak titik Oke titik Byang dalam hal ini merupakan jari-jari lingkaran. Jari-jari lingkaran biasanya dilambangkan dengan r.

Diameter lingkaran adalah panjang ruas garis lurus yang melalui titik pusat dan menghubungkan dua buah titik pada lingkaran. Sebagai contoh, perhatikan gambar lingkaran berikut ini.

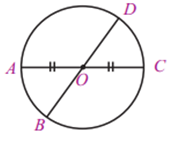
Titik pusat lingkaran pada gambar di atas adalah O. Titik A, B, C, dan Dada pada lingkaran. Ruas garis AC dan BD melalui titik O. Panjang ruas garis AC sama dengan ruas garis BDyang merupakan diameter lingkaran tersebut.

Diameter lingkaran dilambangkan dengan d. Diameter lingkaran sama dengan dua kali jari-jarinya. Dengan demikian,

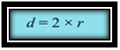
2. Nilai π dan Keliling lingkaran

Sebuah taman berbentuk lingkaran memiliki diameter 10 meter. Roni berlari mengelilingi taman itu satu kali putaran. Berapa meter jarak yang telah ditempuh Ali? Jarak yang ditempuh Ali sama dengan keliling taman yang berbentuk lingkaran tersebut. Dapatkah kamu mencari keliling lingkaran jika diketahui diameternya?Agar kamu dapat menjawabnya, lakukanlah kegiatan berikut.

a.    Sediakan benda-benda yang berbentuk lingkaran. Misaluang logam, tutup toples, tutup gelas, kaleng susu yang alasnya berbentuk lingkaran.,

b.    Ukurlahgaris tengah dari uang logam yang berbentuk lingkaran seperti gambar berikut. Kemudian tulislah garis tengahnya( diameter), d = … cm

c.    Lingkarkan benang sepanjang keliling benda beralas bentuk lingkaran tersebut, kemudian bentangan benang itu dan ukurlah panjangnya. Panjang benang tersebut sama dengan keliling lingkaran, K = … cm

d.   Bagilah keliling lingkaran (K) dengan diameter (d)

e.    Ukurlah diameter dan keliling dari benda lain yang beralas lingkaran tersebut,kemudian buatlah tabel seperti berikut

No	Nama Benda	Diameter (d)	Keliling (K)
1	Uang logam	… cm	… cm	…
2	Tutup toples	… cm	… cm	…
3	Tutup gelas	… cm	… cm	…
4	…	… cm	… cm	…

Dari kegiatan tersebut, kamu akan mendapatkan bahwa perbandingan yang konstan antara keliling (K) dan diameter lingkaran (d) mendekati bilangan 3,14159265358 (3,14)atau 22/7. Selanjutnya, bilangan ini dinamakan π, dibaca pi.

:

Dapat dilihat pada gambar di atas bahwa terdapat lingkaran yang berwarna merah dan di dalamnya terdapat garis berwarna hijau yang menandakan putaran. Anggap saja lingkaran tersebut adalah sebuah lapangan dimana kita disuruh berlari mengelilinginya, maka apabila kita disuruh berlari mengelilingi lapangan sebanyak 1 kali hal ini berarti kita harus berlari dari titik A hingga sampai ke titik A lagi.

Atau kita dapat memisalkan lingkaran tersebut adalah sebuah tali yang dibentuk menyerupai sebuah lingkaran. jika lingkaran itu merupakan sebuah tali maka ketika lingkaran tersebut kitabuka, maka keliling lingkaran merupakan panjang dari tali yang membentuk lingkaran tersebut.

Karena                         π = K/d

Dengan demikian, diperoleh

Oleh karena                                         d = 2 x r

Maka keliling lingkaran dapat juga dirumuskan sebagai berikut.

ContohSoal:

3. Luas Lingkaran

Pengertian luas lingkaran di sini adalah luas daerah yang dibatasi oleh lingkarantersebut. Luas lingkaran adalah area yang terdapat didalam suatu lingkaran. Cara mencari area dari suatu lingkaran dengan melakukan kegiatan:

a.     Buatlahlingkarandengan r = 10 cm

b.    Bagilahlingkarantersebutmenjadi 2 bagian yang samadengancaramembuat diameter danberilahwarna yang berbeda.

c.     Bagilah lingkaran itu menjadi juring-juring dengan besar sudut sanma besar. Menjadi 16 juring

d.    Bagilah salah satu juring yang terjadi menjadi dua bagian yang sama.

e.     Guntinglah lingkaran tersebut sesuai dengan juring-juring yang terjadi.

f. Letakan potongan-potongan dari juring-juring tersebut secara berdampingan seperti gambar di bawah ini:

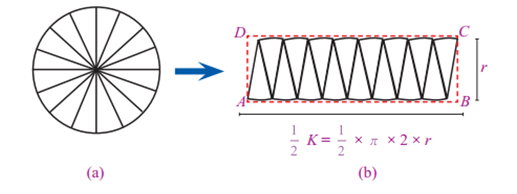
Dari kegiatan di atas didapat

a.    Sebuah lingkaran dibagi menjadi beberapa bagian. Pada gambar ini tampak bahwa lingkaran dibagi menjadi 16 bagian.

b.    Bagian-bagian lingkaran disusun menyerupai persegi panjang dengan lebar sama dengan jari-jari lingkaran, yaitu r. Adapun panjangnya adalah setengah dari keliling lingkaran atau 1/2 K

Dari gambar tersebut, diperoleh bahwa luas lingkaran mendekati luas persegi panjang dengan panjang 1/2 K dan lebar r.

Luas lingkaran = luas persegi panjang ABCD

Jadi, luas lingkaran adalah

Dari hubungan d = 2r atau r = 1/2 d

Maka r² = 1/2 x 1/2 d^2

            = 1/4 d^4

Didapatkan 

Silahkan mencoba menyusun potongan-potongan juring menjadi bangun datar yang lainnya dan temukanlah rumus luas lingkaran.

Misal :

Luas segitiga   = 1/2 alas x tinggi

                                    = 1/2 . (1/4 K  .4r)

                                    = 1/2 . (1/4 2 phi r. 4r)

                                    = 1/2 (2 phi r^2)

                                    = phi r^2

Luas belah ketupat      = alasx tinggi
                                                = 1/4 K  .2r
                                                = 1/4 x 2 phi r. 2r
                                                = 2 phi r

ContohSoal

1.   Hitunglahluaslingkaranjikadiketahuisepertigambarberikut :

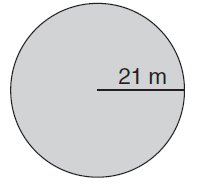
Diketahui :

r = 21 m

Ditanya :

LuasLingkaran= ?

Jawab :

LuasLingkaran = π . r²

2.   Hitunglahluaslingkaran yang diameternya 10 cm!!

Jawaban:
Diameter = 2 x r. Makajari-jarinyaadalah = 5 cm. Dengandemikian, luasnyaadalah

LuasLingkaran = π . r²

 =

Selain itu dengan cara

Luas lingkaran = ×π × 

                                                =  x x 10²

                                                                = 78, 5 cm²

B. SEGI BANYAK

Suatu bangun disebut segitiga karena mempunyai tiga sisi. Disebut segi empat karena mempunyai empat sisi.Bangun datar yang ada di papan tulis di depandisebut bangun segi banyak. Tahukah kamu kenapa disebut segi banyak? Bangun-bangun tersebut disebut segi banyak karena mempunyai sisi sebanyak lima atau lebih.

1.      KelilingSegiBanyak

Cara menghitungkelilingsegibanyakyaitudengancaramenjumlahkansemuapanjangsisi yang mengitaribangundatartersebut.

Perhatikancontohberikut.

Cara menghitungkelilingbangun di atasyaitudenganmenjumlahkansemuapanjangsisi yang mengelilingibanguntersebut.

Panjang AB = 30 cm

Panjang BC = 7 cm

Panjang CD = panjang AB – panjang EF

 = 30 cm – 7 cm

 = 23 cm

Panjang DE = 7 cm

Panjang EF = 7 cm

Panjang FA = panjang DE + panjang BC

 = 7 cm + 7 cm

 = 14 cm

Keliling = AB + BC + CD + DE + EF + FA

= 30 cm + 7 cm + 23 cm + 7 cm + 7 cm + 14 cm

= 88 cm

2.      LuasSegiBanyak

Bagaimana cara menghitung luas segi banyak?Cara menghitungnya dengan menjumlahkan luas bangun-bangun sederhana yang membentuknya. Coba lakukan kegiatan berikut.

Bangun datar pada Gambar (a) dan (b) dinamakan juga segi banyak. Bangun (a) dibentuk oleh persegipanjang dan persegi. Adapun bangun (b) dibentuk oleh persegipanjang dan segitiga. Bagaimanakah cara menghitung luas segi banyak tersebut?

Langkah-langkah untuk menghitung luas segi banyak adalah sebagai berikut.

1.      Tentukan bangun datar apa saja yang membentuknya.

2.      Tentukan luas dari setiap bangun datar yang membentuknya

3.      Jumlahkan luas dari keseluruhan bangun datar yang membentuknya.

Berdasarkan langkah-langkah tersebut, maka

• Luas bangun (a)

Langkah 1:

Membagi segi banyak. Segi banyak di samping dapat dibagi menjadi bangun Persegi dan Persegi Panjang

Langkah 2:

Menghitung luas tiap bagian.

Luas persegipanjang    = p x l

                                    = 10 cm x 4 cm

                                    = 40 cm²

Luas persegi                = s x s

                                    = 3 cm x 3 cm

                                    = 9 cm²

Langkah 3:

Menjumlahkan luasnya

Luas segi banyak         = luas persegi panjang + luas persegi

                                    = 40 cm^{2 +} 9 cm²

                                    = 49 cm²

• Luas bangun (b)

Langkah 1:

Membagi segi banyak. Segi banyak di samping dapat dibagi menjadi bangun Persegi Panjang dan segitiga.

Langkah 2:

Menghitung luas tiap bagian.

Luas persegipanjang    = p x l

                                    = 12 cm x 8 cm

                                    = 96 cm²

Luas segitiga               = . a . t

                                    =  x 8 cm x 3 cm

                                    = 12 cm²

Langkah 3:

Menjumlahkan luasnya

Luas segi banyak         = luas persegi panjang + luas segitiga

                                    = 96 cm^{2 +} 12 cm²

                                    = 108 cm²

Agar kamu lebih memahami dalam menghitung luas segi banyak, pelajarilah contoh berikut.

3.      Menghitung Luas BangunGabunganBangunDatar

Perhatikan gambar bangun-bangun di atas.

Bangun-bangun itu merupakan gabungan dari beberapa bangun datar sederhana. Cara mencari luas bangun gabungan sama dengan mencari luas segi banyak. Caranya membagi menjadi beberapa bangun datar sederhana kemudian menghitung luas masing-masing bangun datar tersebut