Daftar isi
Gerbang Logika
Gerbang logika adalah dasar dari sistem elektronika digital yang berfungsi untuk mengubah input menjadi sebuah sinyal output yang logis. Gerbang logika memiliki 7 jenis gerbang logika, adalah sebagai berikut :
1. AND
adalah apabila semua atau salah satu input merupakan bilangan biner berlogika 0, maka output akan menjadi 0. Sedangkan jika semua input adalah bilangan biner berlogika 1, maka output akan berlogika 1

Gambar : Simbol Logika dan Tabel AND
2. OR
adalah apabila semua atau salah satu input merupakan bilangan biner berlogika 1, maka output akan menjadi 1. Sedangkan jika input adalah bilangan biner yang berlogika 0, maka outputnya akan berlogika 0

Gambar : Simbol Logika dan Tabel OR
3. NOT
fungsi gerbang NOT adalah sebagai inverter atau pembalik, dimana nilai outputnya akan berlawanan dengan inputnya. Jika bilangan biner inputannya bernilai 1, maka nilai outputnya akan bernilai 0. Begitu juga sebaliknya
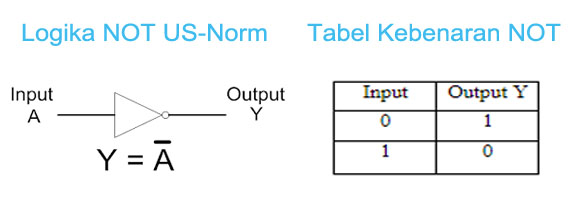
Gambar : Simbol Logika dan Tabel NOT
4. NAND
adalah gabungan dari logika AND dan NOT, yang berarti outputan NAND adalah hasil logika AND yang di-NOT-kan. Sehingga apabila semua atau salah satu input bilangan biner berlogika 0, maka outputnya akan berlogika 1. Sedangkan jika semua input adalah bilangan biner berlogika 1, maka output akan berlogika 0.
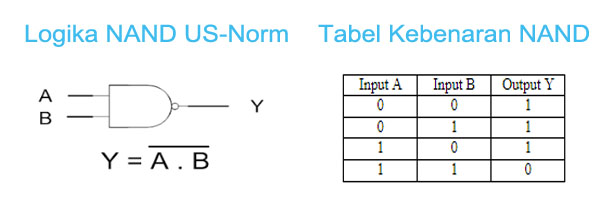
Gerbang : Simbol Logika dan Tabel NAND
5. NOR
adalah gabungan logika OR dan NOT apabila semua atau salah satu input bilangan biner berlogika 1, maka outputnya akan berlogika 0. Sedangkan jika semua input adalah bilangan biner berlogika 0, maka outputnya berlogika 1.
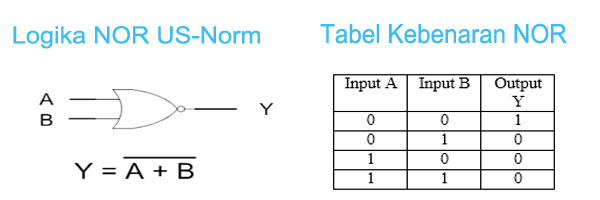
Gambar : Simbol Logika dan Tabel NOR
6. XOR
adalah apabila input berbeda (contoh ; input A=1, input B=0) maka output akan berlogika 1. Sedangkan jika input adalah sama, maka output akan berlogika 0.

Gambar : Simbol Logika dan Tabel XOR
7. Gerbang logika XNOR
apabila input berbeda (contoh; input A=1, input B=0) maka ouput akan berlogika 0. Sedangkan jika input adalah sama, maka output akan berlogika 1.

Gambar : Simbol Logika dan Tabel XNOR
Aturan Boolean
Aturan Boolean atau Aljabar Boolean digunakan untuk menganalisa dan menyederhanakan sirkuit logika digital. Aljabar Boolean hanya digunakan angka biner 1 dan 0 yang disebut juga Aljabar Biner atau Aljabar logika. Aturan Boolean diciptakan oleh Goerge Boole pada tahun 1854.
Berikut ini aturan penting dalam Aljabar Boolean :
- Variabel yang digunakan hanya memiliki dua nilai. Biner 1 untuk ON/HIGH dan Biner 0 untuk OFF/LOW
- Komplemen atau not dari suatu variable diwakili oleh sebuah strip di atas (-) diatas variable. Dimana komplemen dari variable Y diwakili, jika Y’ = 1 maka, Y = 0 dan jika Y = 1 maka Y’ = 0.
- Variabel OR diwakili oleh (+) diantara variable. Contoh variable O; X, Y, Z diwakili X+Y+Z
- Logika AND pada variable dua atau lebih diwakili dengan menuliskan titik diantara variable, seperti variable X.Y.Z terkadang tidak diberi titik, hanya XYZ
Seperti yang dilampirkan pada Tabel berikut :

Gambar : Tabel Aturan Boolean
Pembuktian untuk Aturan Distributive :
X. (Y+Z) = (X.Y) + (X.Y)
Pembuktian :
X + (Y.Z) = X.1 + Y.Z (karena, X.1 = X)
= X.(1+Y) + Y.Z (Karena, Y+1 = 1)
= X.1 + XY + YZ
= X.(1+Z) + XY + YZ (karena, X.X = 1 = X)
= X.(X+Z) + Y.(X+Z)
=(X+Y).(X+Y)
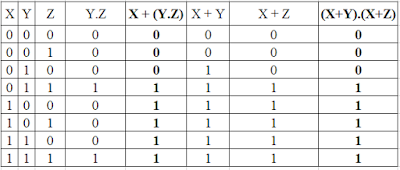
Gambar : Tabel Pembuktian Aturan Distributive

Gambar : Gerbang Logika Aturan Distributive
Dan Terbukti Aturan Aljabar Boolean Distributive adalah benar.
2 Contoh Penerapan aturan Boolean

Penyelesaian 1.

Gambar : Tabel Kebenaran Sebelum diselesaikan

Gambar : Gerbang Logika sebelum disedernakan
Penyederhanaan persamaan menggunakan aturan aljabar Boolean ;


Gambar : Tabel Kebenaran Setelah disederhanakan

Gambar : Gerbang Logika Setelah disederhanakan
Penjelesan 2.

Gambar : Tabel Kebenaran sebelum disederhanakan

Gambar : Gerbang Logika Sebelum disederhanakan
Penyederhanaan persamaan menggunakan aturan Aljabar Boolean


Gambar : Tabel kebenaran Setelah disederhanakan

Gambar : Gerbang Logika setelah disederhanakan
Teori De Morgan
Pernyataan “ Jika dan hanya jika semua masukan adalah benar (1), maka keluarannya adalah benar (1)”. Secara logika ekiuvalen dengan pernyataan “jika salah satu saja dari masukannya berlogika 0, maka outputnya 0”. Aljabar Boolean sebagai aljabar logika mempunyai banyak aturan atau teori. Salah satu teori yang sangat berguna adalah teori De Morgan. Dengan teori ini, memungkinkan kita dapat mengubah secara bolak balik dengan mudah dari bentuk pernyataan Boolean. Teori ini di sebut juga dapat digunakan untuk menghilangkan tanda strip (tanda komplemen) diatas beberapa variable.



Macam macam ekpresi Boolean
POS (marxterm) ; merupakan perkalian dari hasil penjumlahan Product of sum adalah metode untuk menentukan ekpresi Boolean atau gerbang logika yang sudah di ketahui tabel kebenarannya. Caranya adalah dengan menyatukan gerbang (product /AND) yang merupakan hasil dari penjumlahan (sum/OR) berbalikan dari metode Sum of product (SOP).
Contoh ; Diketahui tabel kebenaran dengan input A,B, dan C. maka tentukan ekpresi Boolean dan gerbang logikanya.

Gambar : Tabel Input A B dan C
Jawab :
1. Untuk menentukan ekspresi Boolean, kita soroti output tabel kebenaran yang mempunyai nilai output 0. Maka ekspresi Boolean dengan metode POS adalah dengan menjumlahkan (SUM/OR) terlebih dahulu, selanjutnya baru dikalikan (Product / AND. Sebelum dijumlahkan, nilai logika inputnya harus bernilai 0, apabila bernilai 1, maka diinversekan terlebih dahulu. Dan ini adalah ekspresi Boolean pada tabel kebenaran di atas. Y = (invA+B+C).(invA+invB+invC)
2. Untuk gerbang logika, kita dapat menentukannya dari ekspresi Boolean yang telah didapat, berikut adalah gerbang logikanya

Gambar : Ekspresi Boleean yang telah didapat
SOP (minterm) ; Merupakan hasil penjumlahan dari hasil perkalian. Sum of product adalah metode untuk menentukan ekspresi Boolean atau gerbang logika yang sudah diketahui kebenarannya. Caranya adalah dengan menyatukan gerbang (sum/OR) yang merupakan hasil dari perkalian (product /AND)
Contoh ; Diketahui tabel kebenaran dengan input A, B, dan C. maka tentukanlah ekspresi Boolean dan gerbang logikanya.

Gambar : Input A B dan C
Jawab :
1. untuk menentukan ekspresi Boolean, kita aoroti output tabel kebenaran yang mempunyai nilai output 1. Maka ekspresi Boolean dengan metode SOP adalah dengan mengalikan (product /AND) terlebih dahulu, selanjutnya baru di jumlahkan (SUM/OR). Sebelum dikalikan, nilai logika input harus bernilai 1, apabila bernilai 0, maka diinversekan terlebih dahulu. Dan ini adalah ekspresi Boolean pada tabel kebenaran di atas Y = (invA.invB.C) + (A.B.C)
2. untuk gerbang logika, kita dapat menentukannya dari ekspresi Boolean yang telah didapat, berikut adalah gerbang logikanya

Gambar : Ekpresi Boolean yang telah didapat
Teori K Map
Karnaugh Map atau K-Map adalah suatu teknik penyederhanaan fungsi logika dengan cara pemetaan. K-map terdiri dari kotak kotak yang jumlahnya terdiri dari jumlah variable dan fungsi logika atau jumlah inputan dar rangkaian logika yang sedang kita hitung.
Rumus untuk menentukan jumblah kotak pada K-Map adalah 2^n yang mana N adalah banyaknya variable.
Langkah pemetaan K-map secara umum ;
menyusun aljabar Boolean terlebih dahulu
menggambar rangkaian digital
membuat tabel kebenaran
merumuskan tabel kebenaran
lalu memasukkan rumus tabel kebenaran ke k-map (kotak-kotak) Contoh penyederhanaan 2 variabel

Yang dapat disederhanakan dalam k-map hanya 2 atau kelipatan 2 dari kotak yang berdempetan dan sedangkan jika seperti kotak diatas maka penyederhanaannya :

Karena kolom ber angka 1 dan bari ber angka 1 memenuhi setiap garisnya, maka dapat disimpulkan kalau
Maka K-mapnya adalah AB/BA.
Begitulah penjelasan dari Gerbang Logika disertai Aturan dan Ekspresi Boolean
Leave a Reply
You must be logged in to post a comment.