Berikut ini adalah laporan praktikum fisika bandul matematis. Praktikum ini bertujuan untuk menghitung percepatan gravitasi Bumi pada lokasi praktikum.
Daftar isi
Bandul Matematis
Bab I. Pendahuluan
A. Latar Belakang
Suatu peristiwa dalam kehidupan sehari hari selalu erat kaitannya dengan ilmu fisika ,diantaranya adalah peristiwa bandul matematis.Prinsip yang digunakan pada peristiwa bandul matematis sangat bermanfaat dalam kehidupan sehari hari. Misalnya pada bola penghantar kabel penderek, timah kecil yang ditahan oleh suatu tali pada tempat pengukuran tanah, ayunan yang terdapat di taman kanak kanak,wahana kapal yang ada di taman bermain seperti di Ancol Jakarta, serta konsep bandul pada jam dinding.
Ayunan merupakan salah satu sistem yang melakukan gerak harmonis sederhana yang memiliki amplitudo kecil.Bandul sederhana adalah benda ideal yang terdiri dari sebuah benda yang bermassa m di gantung pada tali yang ringan, dengan catatan panjang tali tersebut tidak akan bertambah saat di beri beban.Bila bandul di geser ke samping dari titi kesetimbangan ( titik tengah ), dan ketika di lepaskan, maka bandul akan berayun dalam bidang vertikal karena di pengaruhi oleh gaya gravitasi bumi. Pada ayunan tersebut nantinya akan dapat di ketahui periode nya, yaitu selang waktu yang dibutuhkan oleh beban untuk melakukan Suatu getaran dan juga menghitung besar Gravitasi bumi di suatu tempat .
Berdasarkan pernyataan pernyataan di atas, maka di lakukanlah percobaan bandul sistematis ini agar dapat di ketahui Prinsip dasar apa saja yang digunakan pada bandul matematis sehingga dapat mengaplikasikannya dalam kehidupan sehari hari.
2. Rumusan Masalah
- Bagaimana memahami azas kerja ayunan / bandul matematis ?
- Bagaimana memahami dan menentukan besar percepatan gravitasi ?
- Bagaimana menentukan besarnya percepatan gravitasi bumi dengan metode ayunan bandul.?
- Bagaimana menentukan pengaruh panjang tali terhadap besarnya periode osilasi bandul.?
- Bagaimana menentukan pengaruh besar simpangan awal terhadap besarnya nilai g yang diperoleh.?
3. Hipotesis
- Semakin pendeknya tali maka gerak bandul akan demakin cepat. Semakin panjang tali maka gerak bandul semakin lambat
- Besar kecilnya nilai percepatan gravitasi tergantung panjang tali dan periode ayunan
- Panjang tali mepengaruhi jarak lintasan
4. Tujuan Percobaan
- Memahami azas kerja ayunan matematis dan getaran selaras.
- Memahami dan menentukan besar percepatan gravitasi ditempat percobaan dilakukan.
- Mengetahui hubungan antara periode bandul matematis dengan panjang tali gantungan
- Mengamati gerak osilasi bandul matematis
- Menentukan frekuensi bandul matematis
- Menganalisis konsep gerak harmonis sederhana dan beberapa faktor yang mempengaruhi periode gerak bandul sederhana
Bab II. Kajian Teori
Pandulum adalah beban yang diikat dengan tali dan di gunakan pada suatu tempat dimana tali yang di gantungkan tidak dapat mulur, jika dengan sudut tertentu kemudian di lepaskan maka benda akan beayun pada bidang vertikal, kerak bolak balik pada bandul di sebut gerak sederhana.
Jika gaya-gaya yang bekerja pada beban diuraikan atas komponen radial dan komponen tangensial, maka resultan gaya radial bertindak sebagai gaya yang dibutuhkan agar beban tetap bergerak melingkar dan resultan gaya tangensial bertindak sebagai gaya pemulih yang bekerja pada beban untuk mengembalikan ke titik kesetimbangannya.
Bandul adalah benda yang terikat pada sebuah tali dan dapat beraun secara bebas dan periodik yang menjadi dasar kerja dari sebuah jam dinding kuno yang mempunyai ayunan.Dalam bidang fisika, prinsip ini pertama kali ditemukan pada tahun 1602 oleh Galileo Galiler,bahwa perioda (lama gerak osilasi satu ayunan, T) dipengaruhi oleh panjang tali danpercepatan gravitasi mengikuti rumus:T= 2π θ ( Sudut – ayunan) >> 1 dimana L adalah panjang tali dan g adalah percepatan gravitasi. (Novitasari,2013)
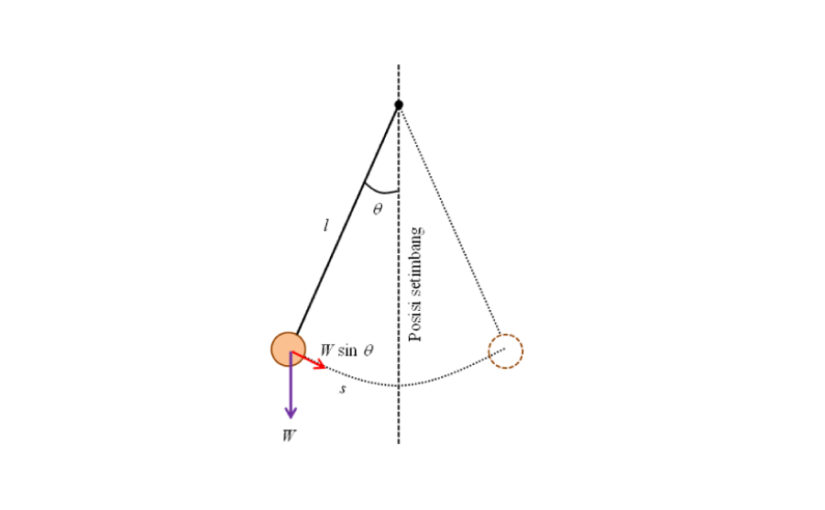
Gaya yang bekerja pada bola pendulum adalah gaya berat (w = mg) dan gaya tegangan tali FT. Gaya berat memiliki komponen mg cos θ yang searah tali dan mg sin θ yang tegak lurus tali. Pendulum berosilasi akibat adanya komponen gaya berat mg sin θ. Karena tidak ada gaya gesek udara, maka pendulum melakukan osilasi sepanjang busur lingkaran dengan besar amplitudo tetap sama (Prihanto, 2013).
Gerakan ayunan bandul sederhana berkaitan dengan panjang tali, sudut awal, massa bandul, amplitudo, dan periode ayunan. Panjang tali yang digunakan untuk mengikat bandul merupakan tali tanpa massa dan tidak dapat mulur. Dan bandul yang digunakan dianggap sebagai massa titik. Jika tidak ada gesekan maka suatu ayunan akan terus berosilasi tanpa berhenti. Namun kenyataannya jika kita mengayunkan bandul, setelah sekian lama amplitudo osilasi teredam dikarenakan adanya gesekan (Khotimah, 2011).
Pada mulanya, dibuat tiga asumsi tentang bandul. Pertama, tali di mana massa beban berayun adalah tidak bermassa, tidak meregang, dan selalu tetap tegang. Kedua, massa beban adalah massa titik. Ketiga, gerak terjadi dalam bidang dua dimensi, yaitu pendulum tidak berayun masuk dan keluar dari bidang. (Sihono, 2007: 18) Online
Perioda ayunan adalah waktu yang dibutuhkan ayunan untuk melakukan satu kali gerakan bolak balik perioda pada ayunan sederhana dipeeroleh oleh persamaan gaya pemulih dan hukum kedua newton, yaitu: – mg sin Ө= m.a (Rustiawan,Suganda,2010:51)
Ketika beban digantungkan pada ayunan dan tidak diberikan gaya maka benda akan diam dititik kesetimbangan B.Jika beban di tarik ke titik A dan dilepaskan,maka beban akan bergerak ke B.C lalu kembali lagi ke A.gerakan beban akan terjadi berulang secara periodik dengan kata lain beban pada ayunan melakukan gerak haarmonik sederhana.
Benda yang bergerka harmonik sederhana pada ayunan sederhana memiliki perioda.Perioda ayunan (T) adalah waktu yang diperlukan benda untuk melakukan satu getaran.Benda dikatakan melakukan getaran jika benda bergerak ke titik dimana benda tersebut mulai bergerak dan kembali lagi ke titik tersebut.( Kartikasari,2014)
Gaya pada partikel sebanding dengan jarak partikel dari posisi setimbang maka partikel tersebut melakukan gerak harmonik sederhana. Teori Robert hooke (1635-1703) menyatkan bahwa jika sebuah benda diubah bentuknya maka benda itu akan melawan perubahan bentuk dengan gaya yang seimbang/sebanding dengan besar deformasi, asalkan deformasi ini tidak terlalu besar, F = -kx. Dan dalam batas elastisitas gaya pada pegas adalah sebanding dengan pertambahan panjang pegas. Sedangkan pertambahan panjang pegas adalah sama dengan simpangan osilasi atau getaran. F = + k∆x
Benda berayun lama akan berhenti bergetar. Ini merupakan periodik teredam. Gerak dengan persamaan berupa fungsi sinus merupakan gerak harmonik sederhana.
Periode getaran yaitu T. Waktu yang diperlukan untuk satu getaran frekuensi gerak f. jumlah getaran dalam satu satuan waktu T = 1/f posisi saat dimana resultan gaya pada benda sama dengan nol adalah posisi setimbang, kedua benda mencapai titik nol (setimbang) selalu pada saat yang sama.
Secara eksperimen besarnya percepatan gravitasi bumi dapat di tentukan dengan metode ayunan matematis seperti berikut ini. Suatu benda di gantungkan pada suatu titik tetap dengan seutas tali yang di anggap tidak bermassa, kemudian di simpangkan sebesar sudut θ terhadap garis vertikal maka gaya yang mengembalikan adalah:
F=-mg \sin θ
Gaya gesekan adalah sebanding dengan kecepatan benda dan mempunyai arah yang berlawanan dengan kecepatan. persamaan gerak dari suatu osilator harmonik teredam dapat diperoleh dari hukum II Newton yaitu F = m.a dimana F adalah jumlah dari gaya balik –kx dan gaya redam yaitu –b dx/dt, b adalah suatu tetapan positif.
Banyak benda yang berosilasi bergerak bolak-balik tidak tepat sama karena gaya gesekan melepaskan tenaga geraknya. Periode T suatu gerak harmonik adalah waktu yang dibutuhkan untuk menempuh suatu lintasan langkah dari geraknya yaitu satu putaran penuh atau satu putar frekwensi gerak adalah V = 1/T .
Satuan SI untuk frekwensi adalah putaran periodik hert. posisi pada saat tidak ada gaya netto yang bekerja pada partikel yang berosilasi adalah posisi setimbang. partikel yang mengalami gerak harmonik bergerak bolak-balik melalui titik yang tenaga potensialnya minimum (setimbang). contoh bandul berayun.
Chritian Haygens (1629-1690) menciptakan : Dalam bandul jam, tenaga dinerikan secara otomatis oleh suatu mekanisme pelepasan untuk menutupi hilangnya tenaga karena gesekan.
Bandul matematis adalah salah satu matematis yangbergerak mengikuti gerak harmonik sederhana. bandul matematis merupakan benda ideal yang terdiri dari sebuah titik massa yang digantungkan pada tali ringan yang tidak bermassa. jika bandul disimpangkan dengan sudut θ dari posisi setimbangnya lalu dilepaskan maka bandul akan berayun pada bidang vertikal karena pengaruh dari gaya gravitasinya.
Gerak harmonik sederhana adalah gerak bolak balik benda melalui suatu titik keseimbangan tertentu dengan banyaknya getaran benda dalam setiap sekon selalu konstan. Gerak harmonik sederhana dapat dibedakan menjadi 2 bagian, yaitu (1) gerak harmonik sederhana linier, misalnya penghisap dalam silinder gas, gerak osilasi air raksa/ air dalam pipa U, gerak horizontal/vertikal.
Ketika beban digantungkan pada ayunan dan tidak diberikan gaya, maka benda akan diam di titik keseimbangan B. Jika beban ditarik ke titik A dan dilepaskan, maka beban akan bergerak ke B, C, lalu kembali lagi ke A. Gerakan benda akan terjadi berulang secara periodik, dengan kata lain beban pada ayunan di atas melakukan gerak harmonik sederhana.
Untuk mengukur percepatan gravitasi dan menentukan hubungan periode getaran (+) dengan panjang tali (l) melalui eksperimen dapat dirancang alat seperti pada gambar 2. Benda diikat dengan benang sepanjang (l), dikaitkan pada statif. Kemudian diayunkan. Dengan mengukur waktu pada 10 ayunan, berlaku :
T = t /10
Syarat sebuah benda melakukan gerak harmoni sederhana adalah apabila gaya pemulih sebanding dengan simpangannya. Apabila gaya pemulih sebanding dengan simpangan x atau sudut maka pendulum melakukan gerak harmonik sederhana.
Gerak pemulih pada sebuah ayunan menyebabakannnya selalu bergerak menuju titik setimbangnya. Periode ayunan tidak berhubungan dengan amplitudo, akan tetapi ditentukan oleh parameter internal yang berkait dengan gaya pemulih pada ayunan tersebut.
Periode adalah selang waktu yang diperlukan oleh suatu benda untuk melakukan satu getaran lengkap. Getaran adalah gerakan bolak balik yang ada disekitar titik keseimbangan dimana kuat lemahnya dipengaruhi besar kecilnya energi.
Bab III. Metode Praktikum
A. Alat Dan Bahan
| No | Alat dan Bahan | Fungsi |
| 1 | 1 set statif | Sebagai penyangga |
| 2 | Penggaris logam | Untuk mengukur panjang tali |
| 3 | Jepit penahan | Untuk menjepit batang statif |
| 4 | Tali nilon | Untuk mengikat beban |
| 5 | Stopwatch | Untuk menghitung waktu osilasi bandul |
| 6 | Beban | Sebagai objek pengamatan atau sebagai pemberat |
| 7 | Busur derajat | Untuk memberi simpangan awal pada bandul |
| 8 | Alat Tulis | Untuk mencatat hasil dari percobaan |
| 9 | Neraca digital | Mengukur massa bandul |
B. Identifikasi Variabel
a) Variabel manipulasi
· Simpangan (ᵒ/cm)
b) Variabel kontrol
· Panjang tali ( cm)
· Massa Bandul (g)
· Jumlah ayunan
c) Variabel respon
· Waktu (s)
C. Definisi Operasional Variabel
a) Variabel manipulasi :
Simpangan adalah bandul yang ditarik dari titik kesetimbangannya, yang di ukur dengan busur derajat , dan memiliki Satuan ukur cm.
b) Variabel kontrol :
Panjang tali adalah panjang tali yang di ukur dari suatu ujung ke ujung yang lain yang diukur dengan menggunakan penggaris dan memiliki satuan cm.
Massa bandul adalah berat bandul yang diukur dengan menggunakan neraca digital dan memiliki satuan gram .
Jumlah ayunan adalah banyak nya ayunan yang dilakukan bandul. Pada percobaan kali ini jumlah ayunan di tentukan yaitu sebanyak 20 perioda.
D. Prosedur Kerja
- Rangkailah alat percobaan
- Tempatkan rangkaian di pinggir meja
- Gunakan bola pejal 50 gram sebagai bandul dan ikat bola tersebut menggunakan tali sepanjang 0.5 meter
- Ikat tali tepat pada lubang gantung
- Siapkan stopwatch
- Berikan simpangan sebesar sudut 10 derajat dari titik setimbang. Ambil salah satu titik sebagai acuan.
- Lepaskan bandul dan hidupkan stopwatch secara bersamaan.
- Setelah itu baru mulai mencatat waktu yang diperlukan untuk 20 ayunan.
- Lakukan hal di atas sebanyak 5 kali agar penghitungannya maksimal.
- Siapkan stopwatch
- Berikan simpangan, kali ini sudut 30 derajat dari titik setimbang. Ambil salah satu titik sebagai acuan
- Lepaskan bandul dan hidupkan stopwatch secara bersamaan. Mulai hitung sebanyak 20 ayunan, dan perhatikan waktu yang diperlukan untuk 20 ayunan
- Lakukan hal tersebut sebanyak 5 kali agar penghitungannya maksimal.
- Siapkan stopwatch.
- Berikan simpangan sebesar sudut 10 derajat dari titik setimbang. Ambil salah satu titik sebagai acuan.
- Lepaskan bandul dan hidupkan stopwatch secara bersamaan. Mulai hitung sebanyak 20 ayunan, dan perhatikan waktu yang diperlukan untuk 20 ayunan.
- Ganti panjang Tali yang tadinya adalah sepanjang 50 cm menjadi 40 cm.
- Berikan simpangan pada bandul sebesar sudut 10 derajat dari titik setimbang,.
- Lepaskan bandul dan hidupkan stopwatch secara bersamaan. Mulai hitung sebanyak 20 ayunan.Kemudian catat hasilnya dalam buku tulis.
- Berikan simpangan pada bandul sebesar sudut 30 derajat dari titik setimbang,.
- Lepaskan bandul dan hidupkan stopwatch secara bersamaan. Mulai hitung sebanyak 20 ayunan. Kemudian catat hasilnya dalam buku tulis.
- Berikan simpangan pada bandul sebesar sudut 45 derajat dari titik setimbang,.
- Lepaskan bandul dan hidupkan stopwatch secara bersamaan. Mulai hitung sebanyak 20 ayunan.Kemudian catat hasilnya dalam buku tulis.
- Lakukakn kegiatan pada nomor 18-23, namun dengan panjang tali yang berbeda, yaitu 30 cm.
Bab IV. Hasil dan Pembahasan
A. Hasil Pengamatan
Kegiatan 1 : Hubungan pengaruh besar simpangan terhadap waktu selama 20 kali gerakan bolak balik bandul.
Berikut ini adalah tabel dari hasil percobaan yang telah dilakukan
| No. | Simpangan Sudut (ᵒ) | Panjang tali (cm) | Beban (g) | Waktu (s) |
| 1 | 10 | 50 | 50 | 29,63 |
| 2 | 50 | 50 | 30,26 | |
| 3 | 50 | 50 | 30,15 | |
| 4 | 50 | 50 | 30,5 | |
| 5 | 50 | 50 | 30,52 | |
| 6 | 30 | 50 | 50 | 30,62 |
| 7 | 50 | 50 | 30,82 | |
| 8 | 50 | 50 | 30,89 | |
| 9 | 50 | 50 | 30,78 | |
| 10 | 50 | 50 | 30,93 | |
| 11 | 45 | 50 | 50 | 31,79 |
| 12 | 50 | 50 | 31,76 | |
| 13 | 50 | 50 | 31,92 | |
| 14 | 50 | 50 | 31,66 | |
| 15 | 50 | 50 | 31,94 |
Analisis Data
Setelah mencatat semua hasil dari pengamatan ,untuk mengetahui percepatan gravitasi bumi dengan menggunakan bandul matematis , terlebih dahulu kita harus mencari periodenya .
Rumus Periode adalah :
T = t/s
Dimana : T = Periode (s)
t = Waktu yang di tempuh berdasar jumlah ayunan (s)
s = Jumlah ayunan bandul
Kemudian kita masukkan rumus berdasarkan teori yang ada , Diketahui suatu rumus percepatan gravitasi. Dimana
g=4 \pi ^2\frac{l}{T^2}Dimana :
g : Percepatan gravitas (m/s2)
l : Panjang tali (m)
T = Perioda (s)
Sekarang kita masukkan rumus tersebut pada hasil percobaan yang telah di lakukan
A. Percobaan dengan simpangan sebesar 10 derajat :
1. Percobaan 1
L 1 =50 cm = 0,5 m
T= t/n = 29,63/20 = 1,4815 s
T2= (1,48)2 = 2,194 s2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,194 = 9,39 m/s2
2. Percobaan 2
L 1 =50 cm = 0,5 m
T= t/n = 30,26/20 = 1,513 s
T2= (1,513)2 = 2,289 s2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,289 = 8,64 m/s2
3. Percobaan 3
L 1 =50 cm = 0,5 m
T= t/n = 30,15/20 = 1,507 s
T2= (1,48)2 = 2,27 S2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,194 = 8,68 m/s2
4. Percobaan 4
L 1 =50 cm = 0,5 m
T= t/n = 29,20/20 = 1,46 s
T2= (1,46)2 = 2,13 s2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,13 = 9,25 m/s2
5. Percobaan 5
L 1 =50 cm = 0,5 m
T= t/n = 28,26/20 = 1,41 s
T2= (1,41)2 = 1,9 s2
G = 4 π2 L / T2 = 4×9,8596×0,5/1,9 = 9,909 m/s2
Dari hasil perhitungan di atas, dapat di ketahui rata rata percepatan gravitasi berdasarkan simpangan 10 derajat adalah :
= 9,17
Dan dapat di ketahui hasil rata rata perioda nya adalah :
= 1,47 s
B. Percobaan dengan simpangan sebesar 30 derajat :
1. Percobaan 1
L 1 =50 cm = 0,5 m
T= t/n = 30,62/20 = 1,53 s
T2= (1,53)2 = 2,34 s2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,34 = 8,427 m/s2
2. Percobaan 2
L 1 =50 cm = 0,5 m
T= t/n = 30,82/20 = 1,54 s
T2= (1,54)2 = 2,37 s2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,37 = 8,32 m/s2
3. Percobaan 3
L 1 =50 cm = 0,5 m
T= t/n = 30,89/20 = 1,544 s
T2= (1,54)2 = 2,385 s2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,385 = 8,26 m/s2
4. Percobaan 4
L 1 =50 cm = 0,5 m
T= t/n = 30,78/20 = 1,539 s
T2= (1,539)2 = 2,368 s2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,368 = 8,327 m/s2
5. Percobaan 5
L 1 =50 cm = 0,5 m
T= t/n = 30,93/20 = 1,546 s
T2= (1,546)2 = 2,39 s2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,39 = 8,25 m/s2
Dari hasil perhitungan di atas , dapat di ketahui rata rata percepatan gravitasi berdasarkan simpangan 30 derajat adalah :
= 8,31m/s2
Dan dapat di ketahui hasil rata rata perioda nya adalah :
= 1,539 s
C. Percobaan dengan simpangan sebesar 45 derajat :
1. Percobaan 1
L 1 =50 cm = 0,5 m
T= t/n = 31,79/20 = 1,58 s
T2= (1,58)2 = 2,52 S2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,52 = 7,82 m/s2
2. Percobaan 2
L 1 =50 cm = 0,5 m
T= t/n = 31,92/20 = 1,596 s
T2= (1,596)2 = 2,54 S2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,54 = 7,76 m/s2
3. Percobaan 3
L 1 =50 cm = 0,5 m
T= t/n = 31,76/20 = 1,58 s
T2= (1,58)2 = 2,52 S2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,385 = 7,82 m/s2
D. Percobaan 4
L 1 =50 cm = 0,5 m
T= t/n = 31,66/20 = 1,58 s
T2= (1,58)2 = 2,52 S2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,52 = 7,82 m/s2
E. Percobaan 5
L 1 =50 cm = 0,5 m
T= t/n = 31,60/20 = 1,58 s
T2= (1,58)2 = 2,52 S2
G = 4 π2 L / T2 = 4×9,8596×0,5/2,52 = 7,82 m/s2
Dari hasil perhitungan di atas , dapat di ketahui rata rata percepatan gravitasi berdasarkan simpangan 45 derajat adalah :
= 7,80m/s2
Dan dapat di ketahui hasil rata rata perioda nya adalah :
= 1,58 s
(Di karenakan hasil yang di peroleh rata rata perbedaannya tidak terlalu signifikan , maka seterusnya hanya akan di lakukan sekali percobaan dengan simpangan yang berbeda .)
Berikut ini adalah tabel perbandingan dari hasil di atas
| No | Simpangan Sudut (ᵒ) | Percepatan Gravitasi | rata rata periode |
| 1 | 10 | 9,17 | 1,47 |
| 2 | 30 | 8,31 | 1,539 |
| 3 | 45 | 7,8 | 1,58 |
Kegiatan 2 : Menyelidiki hubungan antara panjang tali dengan Percepatan gravitasi melalui bandul matematis dengan 20 gerakan bolak balik bandul .
Berikut ini adalah tabel dari hasil yang dilakukan dengan mengubah panjang talinya yaitu ukuran panjang 40 cm dan 30 cm
| No. | Simpangan Sudut (ᵒ) | Panjang tali ( cm) | Beban (gram) | Waktu(s) |
| 1 | 10 | 40 | 50 | 27,93 |
| 2 | 30 | 50 | 25,3 | |
| 3 | 30 | 40 | 50 | 28,33 |
| 4 | 30 | 50 | 25,73 | |
| 5 | 45 | 40 | 50 | 28,99 |
| 6 | 30 | 50 | 26,28 |
Percobaan dengan Panjang tali 40 cm :
1. Percobaan 1 dengan simpangan 10 derajat.
L 1 =40 cm = 0,4 m
T= t/n = 27,93/20 = 1,39 s
T2= (1,39)2 = 1,95 S2
G = 4 π2 L / T2 = 4×9,8596×0,4/1,95 = 8,08 m/s2
2. Percobaan 2 dengan simpangan 30 derajat
L 1 =40 cm = 0,4 m
T= t/n = 28,33/20 = 1,41 s
T2= (1,41)2 = 2,006 S2
G = 4 π2 L / T2 = 4×9,8596×0,4/2,006 = 7,86 m/s2
3. Percobaan 3 dengan simpangan 45 derajat
L 1 =40 cm = 0,4 m
T= t/n = 28,99/20 = 1,4495 s
T2= (1,4495)2 = 2,101 S2
G = 4 π2 L / T2 = 4×9,8596×0,4/2,101 = 7,50 m/s2
Percobaan dengan Panjang tali 30 cm :
1. Percobaan 1 dengan simpangan 10 derajat.
L 1 =30 cm = 0,3 m
T= t/n = 25,30/20 = 1,265 s
T2= (1,265)2 = 1,60 S2
G = 4 π2 L / T2 = 4×9,8596×0,3/1,60 = 7,39 m/s2
2. Percobaan 2 dengan simpangan 30 derajat
L 1 =30 cm = 0,3 m
T= t/n = 25,73/20 = 1,2865 s
T2= (1,2865)2 = 1,655 S2
G = 4 π2 L / T2 = 4×9,8596×0,3/1,655 = 7,14 m/s2
3. Percobaan 3 dengan simpangan 45 derajat
L 1 =30 cm = 0,3 m
T= t/n = 26,28/20 = 1,314 s
T2= (1,314)2 = 1,726 S2
G = 4 π2 L / T2 = 4×9,8596×0,3/1,726 = 6,85 m/s2
Berikut ini adalah tabel hasil perhitungan perioda dan percepatan gravitasi dari keseluruhan percobaan:
| No. | Panjang Tali | Simpangan | Perioda | Percepatan Gravitasi |
| 1 | 50 | 10 | 1,47 | 9,17 |
| 2 | 30 | 1,539 | 8,31 | |
| 3 | 45 | 1,58 | 7,8 | |
| 4 | 40 | 10 | 1,39 | 8,08 |
| 5 | 30 | 1,41 | 7,86 | |
| 6 | 45 | 1,4495 | 7,5 | |
| 7 | 30 | 10 | 1,265 | 7,39 |
| 8 | 30 | 1,2865 | 7,14 | |
| 9 | 45 | 1,314 | 6,85 |
Berikut ini adalah hubungan antara panjang tali, simpangan, beserta perioda yang di sajikan dalam diagram garis:
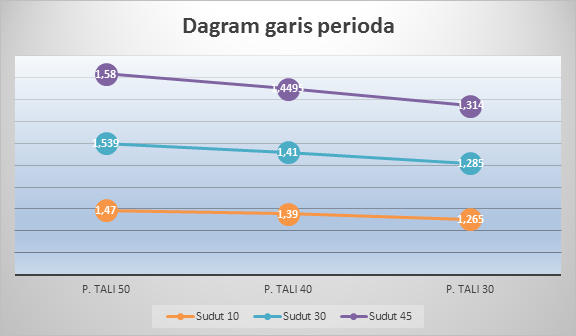
Berikut ini adalah hubungan antara panjang tali, simpangan, beserta percepatan gravitasi yang di sajikan dalam diagram garis:
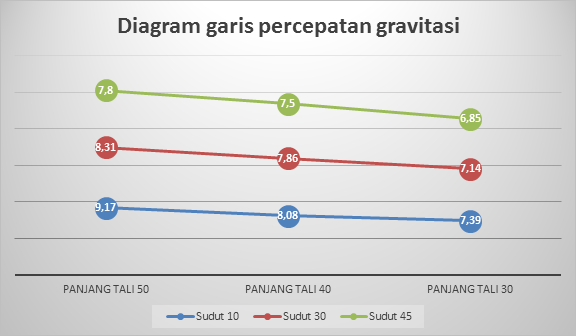
Pengujian Rumus
Untuk Membuktikan bahwa percobaan yang di lakukan sudah berhasil atau tidak, maka perlu diadakan sebuah perbandingan rumus yang ada dalam teori dengan rumus yang ada dalam praktek. Diketahui Rumus dalam teori
T=2 π
Kemudian kita masukkan secara acak dari hasil percobaan yang telah di lakukan :
I. Hasil Percobaan Pada Panjang tali 50 cm dan simpangan 10 derajat
T=2 π
T=2 . 3,14
T=6,28.
T=6,28 x 0,233
T=1,466
Pada Perbandingan antara hasil teori dengan praktek terdapat selisih 0,004 , maka kita anggap percobaan kita kali ini BERHASIL karena angka toleransi nya tidak mencapai kalibrasi dari stopwatch yang di gunakan ( kalibrasi stopwatch 0,01)
Hasil Percobaan Pada Panjang tali 40 cm dan simpangan 30 derajat
T=2 π
T=2 . 3,14
T=6,28.
T=6,28 x 0,2255
T=1,41
Pada Perbandingan antara hasil teori dengan praktek tidak terdapat selisih , maka kita anggap percobaan kita kali ini BERHASIL .
Hasil Percobaan Pada Panjang tali 30 cm dan simpangan 45 derajat
T=2 π
T=2 . 3,14
T=6,28.
T=6,28 x 0,20927
T=1,314
Pada Perbandingan antara hasil teori dengan praktek tidak terdapat selisih , maka kita anggap percobaan kita kali ini BERHASIL .
ANALISIS DAN PEMBAHASAN
Gerak ayunan bandul sederhana berkaitan dengan panjang tali ,sudut awal,massa bandul,amplitudo dan prioda ayunan bandul.Panjang tali yang digunakan untuk mengikat bandu l merupakan tai massa dan tidak dapat mulur.Dan bandul yang digunakan dianggap sebagai massa titik.Jika tidak ada gesekan maka suatu ayunan akan terus berisolasi tanpa berhenti.
Pada percobaan penentuan percepatan gravitasi bumi dengan metode ayunan bandul, dilakukan percobaan sebanyak 21 kali dengan catatan 15 kali percobaan pada panjang tali 50 cm, dan 3 kali percobaan masing masing pada panjang 40cm dan 30cm. Tujuan di adakan percobaan panjang 50 cm sebanyak 15 kali adalah untuk mengukur tingkat keakuratan dari percobaan. Dalam percobaan kali ini , menggunakan simpangan sebesar 10,30 dan 40 derajat, tetapi massa benda yang digunakan pada percobaan ini sama. Pada percobaan ini jumlah ayunan atau osilasi pada tiap-tiap percobaan yaitu 20 kali sehingga diperoleh waktu rata-rata untuk panjang tali 0,5 m secara berturut-turut yaitu 30,26 s ,30,78s, 31,79. Pada panjang tali 0,4 m diperoleh waktu benda untuk berosilasi yaitu 27,93s, 28,33s, 28,99s. Sedangkan dengan panjang tali 0,3 m diperoleh waktu benda untuk berosilasi yaitu 25,30s, 25,7s, 26,28s. Dari data tersebut semakin besar panjang tali dan simpangan yang diberikan maka semakin banyak waktu yang diperlukan benda untuk berosilasi.
Analisis data pada penentuan periode osilasi bandul dilakukan secara praktek dan teori. Secara praktek nilai periode diperoleh dari hasil bagi antara waktu rata-rata dan banyaknya osilasi yang terjadi. Untuk panjang tali 0,5 m diperoleh nilai berturut-turut yaitu 1,47s,1,539s, 1,58s, untuk panjang tali 0,4 m diperoleh 1,39s, 1,41s, 1,44s, dan untuk panjang tali 0,3 m diperoleh nilai periode osilasi berturut-turut yaitu 1,26 s, 1,28 s, dan 1,314 s. Sedangkan secara teori nilai periode osilasi diperoleh dari hasil kali antara dua phi dengan akar dari panjang tali dibagi percepatan gravitasi sehingga diperoleh nilai berturut-turut yaitu 1,466 untuk panjang tali 50 cm dan simpangan 10, dan 1,41 untuk panjang tali 40 cm dan simpangan sebesar 30, serta 1,314 untuk panjang tali 30cm dan simpangan sebesar 45. Dari data tersebut, secara praktek diketahui bahwa periode osilasi berbanding lurus dengan waktu osilasi bandul artinya semakin banyak waktu yang dibutuhkan bandul untuk berosilasi maka semakin besar pula nilai periode yang diperoleh sedangkan secara teori diketahui bahwa periode osilasi berbanding lurus dengan panjang tali yang digunakan artinya semakin besar panjang tali yang digunakan maka semakin besar pula nilai periode yang diperoleh. Periode yang diperoleh secara praktek dan teori berbeda, hal ini dikarenakan kurangnya ketelitian pada saat pengukuran panjang tali, dan perhitungan banyaknya osilasi tidak tepat pada saat menekan stopwatch.
Analisis data pada penentuan percepatan gravitasi dilakukan secara praktek dan teori. Secara praktek nilai percepatan gravitasi diperoleh dari hasil bagi antara empat phi kuadrat dikali panjang tali dan periode kuadrat, sehingga diperoleh nilai percepatan gravitasi berturut-turut yaitu untuk simpangan 10 derajat 9,17 m/s2, 8,08 m/s2, 7,39 m/s2, dan untuk simpangan 30 derajat 8,31m/s2, 7,86 m/s2, 7,14m/s2, serta untuk simpangan 45 derajat sebesar 7,8 m/s2, 7,5 m/s2 dan 6,85m/s2.
Dari data tersebut nilai percepatan gravitasi bumi secara praktek berbanding lurus dengan panjang tali artinya bahwa semakin panjang tali yang digunakan maka semakin besar pula nilai percepatan gravitasi yang diperoleh, sedangkan secara teori percepatan gravitasi berbanding terbalik dengan percepatan bandul artinya semakin besar percepatan bandul maka semakin kecil nilai percepatan gravitasi yang diperoleh. Nilai percepatan gravitasi secara praktek dan teori mengalami perbedaan yang cukup jauh. Hal ini disebabkan oleh beberapa faktor seperti adanya gesekan antara tali dengan udara (angin) yang mempengaruhi benda bergerak bolak-balik atau berosilasi tidak sama, dan kurangnya ketelitian pada saat melakukan praktikum seperti kurang teliti saat mengukur, menghitung waktu osilasi, dan adanya gaya tambahan saat bandul berayun atau berosilasi.
Pada praktikum ini dari analisis data yang diperoleh dapat digambarkan grafik hubungan antara panjang tali (L) dan periode (T2). Dari data tersebut diketahui bahwa periode berbanding lurus dengan panjang tali artinya semakin panjang tali yang digunakan maka semakin besar pula nilai periode yang diperoleh.
Bab V. Penutup
A. Kesimpulan
Pendulum adalah beban yang diikat dengan tali dan digantungkan pada suatu tempat,dimana tali yang digantungkan tidak dapat mulur.Percepatan gravitasi dipengaruhi olleh panjang tali dan perioda seperti persamaan berikut: dimana panjang tali dalam meter (m) dan perioda (T) dalam sekon (s)
Perioda adalah waktu yang digunakan untuk melakukan satu kali gerakan bolak balik.Hal ini menunjukkan dengan gerakan benda dari titk dimana benda tersebut mulai bergerak dan kembali lagi ketitik tersebut.
Periode osilasi bandul berbanding lurus dengan panjang tali artinya semakin panjang tali yang digunakan maka semakin besar pula periode osilasi bandul yang diperoleh.
Simpangan awal berpengaruh dalam menentukan nilai percepatan gravitasi yang diperoleh secara praktek. Sedangkan secara teroi besarnya simpangan awal yang diberikan tidak mempengaruhi besarnya nilai percepatan gravitasi.
Percepatan gravitasi bumi selalu sama jika dihitung secara teori meskipun menggunakan besar simpangan yang berbeda.
B. Saran
Pada pratikum kali ini diharapkan kepada para peserta agar memahami materi yang kan dipraktikkan agar mempermudah menjalankan pratikum,serta penggunaan waktu yang disediakan dapat dioptimalkan dengan baik.
Sebaiknya melakukan percobaan dengan waktu minimal 60 menit agar percobaan berjalan secara maksimal.
Lebih banyak perhitungan dalam satu waktu percobaan akan semakin baik , yang nantinya akan di gunakan nilai rata rata .
Dalam melakukan percobaan sebaiknya dalam ruangan yang tenang , tidak di arahkan ke kipas angin atau sesuatu yang dapat mempengaruhi gerak bandul
DAFTAR PUSTAKA
– Kartikasari,Widya.2014.Laporan Pratikum Bandul sederhana (online).
http//widyawidiwks.blogspot.co.id/2014/03/laporan-pratikum-fisika-percobaan.html ? m=I.
(Diakses pada minggu,1-11-2015,jam 06.32 WIB)
– Novitasari,Elsha.2013.Laporan Fisika Ayunan Bandul sederhana (online).
HHTP://Elshanovitasari.blogspot.com/2013/03/laporan-fisika-ayunan-bandul-sederhana.html? m=I
(Diakses pada minggu 1-11-2015,jam 06.40 WIB).
– Saripudin,Aip,Dede Rustiawan,dan Adit Suganda.2010.Praktis Belajar Fisika. Jakarta : Visindo.
– Tim penyususn panduan pratikum Fisika Dasar.2013. Panduan Pratikum Fisika Dasar.Jambi : Universitas Jambi
Leave a Reply
You must be logged in to post a comment.